WarpX
Loading...
Searching...
No Matches
Public Member Functions | Public Attributes | List of all members
ElectrostaticSolver Class Referenceabstract

Base class for Electrostatic Solver. More...

#include <ElectrostaticSolver.H>

Inheritance diagram for ElectrostaticSolver:
EffectivePotentialES LabFrameExplicitES RelativisticExplicitES

Public Member Functions

 ElectrostaticSolver ()=default
 
 ElectrostaticSolver (int nlevs_max)
 
virtual ~ElectrostaticSolver ()
 
 ElectrostaticSolver (const ElectrostaticSolver &)=delete
 
ElectrostaticSolver & operator= (const ElectrostaticSolver &)=delete
 
 ElectrostaticSolver (ElectrostaticSolver &&)=delete
 
ElectrostaticSolver & operator= (ElectrostaticSolver &&)=delete
 
void ReadParameters ()
 
virtual void InitData ()
 
virtual void ComputeSpaceChargeField (ablastr::fields::MultiFabRegister &fields, MultiParticleContainer &mpc, MultiFluidContainer *mfl, int max_level)=0
 Computes charge density, rho, and solves Poisson's equation to obtain the associated electrostatic potential, phi. Using the electrostatic potential, the electric field is computed in lab frame, and if relativistic, then the electric and magnetic fields are computed using potential, phi, and velocity of source for potential, beta. This function must be defined in the derived classes.
 
void setPhiBC (ablastr::fields::MultiLevelScalarField const &phi, amrex::Real t) const
 Set Dirichlet boundary conditions for the electrostatic solver. The given potential's values are fixed on the boundaries of the given dimension according to the desired values from the simulation input file, boundary.potential_lo and boundary.potential_hi.
 
void computePhi (ablastr::fields::MultiLevelScalarField const &rho, ablastr::fields::MultiLevelScalarField const &phi, std::array< amrex::Real, 3 > beta, amrex::Real required_precision, amrex::Real absolute_tolerance, int max_iters, int verbosity, bool is_igf_2d_slices, std::optional< ablastr::fields::MultiLevelVectorField > efield=std::nullopt) const
 
void computeE (ablastr::fields::MultiLevelVectorField const &E, ablastr::fields::MultiLevelScalarField const &phi, std::array< amrex::Real, 3 > beta) const
 Compute the electric field that corresponds to phi, and add it to the set of MultiFab E. The electric field is calculated by assuming that the source that produces the phi potential is moving with a constant speed $\vec{\beta}$:
 
void computeB (ablastr::fields::MultiLevelVectorField const &B, ablastr::fields::MultiLevelScalarField const &phi, std::array< amrex::Real, 3 > beta) const
 Compute the magnetic field that corresponds to phi, and add it to the set of MultiFab B. The magnetic field is calculated by assuming that the source that produces the phi potential is moving with a constant speed $\vec{\beta}$:
 

Public Attributes

int num_levels
 
std::unique_ptr< PoissonBoundaryHandler > m_poisson_boundary_handler
 
amrex::Real self_fields_required_precision = 1e-11
 
amrex::Real self_fields_absolute_tolerance = 0.0
 
int self_fields_max_iters = 200
 
int self_fields_verbosity = 2
 
bool is_igf_2d_slices = false
 

Detailed Description

Base class for Electrostatic Solver.

Constructor & Destructor Documentation

◆ ElectrostaticSolver() [1/4]

ElectrostaticSolver::ElectrostaticSolver ( )
default

◆ ElectrostaticSolver() [2/4]

ElectrostaticSolver::ElectrostaticSolver ( int nlevs_max)

◆ ~ElectrostaticSolver()

ElectrostaticSolver::~ElectrostaticSolver ( )
virtualdefault

◆ ElectrostaticSolver() [3/4]

ElectrostaticSolver::ElectrostaticSolver ( const ElectrostaticSolver & )
delete

◆ ElectrostaticSolver() [4/4]

ElectrostaticSolver::ElectrostaticSolver ( ElectrostaticSolver && )
delete

Member Function Documentation

◆ computeB()

void ElectrostaticSolver::computeB ( ablastr::fields::MultiLevelVectorField const & B,
ablastr::fields::MultiLevelScalarField const & phi,
std::array< amrex::Real, 3 > beta ) const

Compute the magnetic field that corresponds to phi, and add it to the set of MultiFab B. The magnetic field is calculated by assuming that the source that produces the phi potential is moving with a constant speed 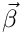$\vec{\beta}$:

\[ \vec{B} = -\frac{1}{c}\vec{\beta}\times\vec{\nabla}\phi *\]

(this represents the term $\vec{\nabla} \times \vec{A}$, in the case of a moving source)

Parameters
[in,out]BElectric field on the grid
[in]phiThe potential from which to compute the electric field
[in]betaRepresents the velocity of the source of phi

◆ computeE()

void ElectrostaticSolver::computeE ( ablastr::fields::MultiLevelVectorField const & E,
ablastr::fields::MultiLevelScalarField const & phi,
std::array< amrex::Real, 3 > beta ) const

Compute the electric field that corresponds to phi, and add it to the set of MultiFab E. The electric field is calculated by assuming that the source that produces the phi potential is moving with a constant speed 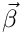$\vec{\beta}$:

\[ \vec{E} = -\vec{\nabla}\phi + \vec{\beta}(\vec{\beta} \cdot \vec{\nabla}\phi) \]

(where the second term represent the term 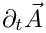$\partial_t \vec{A}$, in the case of a moving source)

Parameters
[in,out]EElectric field on the grid
[in]phiThe potential from which to compute the electric field
[in]betaRepresents the velocity of the source of phi

◆ computePhi()

void ElectrostaticSolver::computePhi ( ablastr::fields::MultiLevelScalarField const & rho,
ablastr::fields::MultiLevelScalarField const & phi,
std::array< amrex::Real, 3 > beta,
amrex::Real required_precision,
amrex::Real absolute_tolerance,
int max_iters,
int verbosity,
bool is_igf_2d_slices,
std::optional< ablastr::fields::MultiLevelVectorField > efield = std::nullopt ) const

Compute the potential phi by solving the Poisson equation with rho as a source, assuming that the source moves at a constant speed 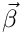$\vec{\beta}$. This uses the amrex solver. More specifically, this solves the equation

\[ \vec{\nabla}^2 r \phi - (\vec{\beta}\cdot\vec{\nabla})^2 r \phi = -\frac{r \rho}{\epsilon_0} \]

Parameters
[in]rhoThe charge density for a given species (relativistic solver) or total charge density (labframe solver)
[out]phiThe potential to be computed by this function
[in]betaRepresents the velocity of the source of phi
[in]required_precisionThe relative convergence threshold for the MLMG solver
[in]absolute_toleranceThe absolute convergence threshold for the MLMG solver
[in]max_itersThe maximum number of iterations allowed for the MLMG solver
[in]verbosityThe verbosity setting for the MLMG solver
[in]is_igf_2d_slicesboolean to select between fully 3D Poisson solver and quasi-3D, i.e. one 2D Poisson solve on every z slice (default: false)
[out]efieldThe electric field corresponding to the calculated phi (only used with embedded boundaries)

◆ ComputeSpaceChargeField()

virtual void ElectrostaticSolver::ComputeSpaceChargeField ( ablastr::fields::MultiFabRegister & fields,
MultiParticleContainer & mpc,
MultiFluidContainer * mfl,
int max_level )
pure virtual

Computes charge density, rho, and solves Poisson's equation to obtain the associated electrostatic potential, phi. Using the electrostatic potential, the electric field is computed in lab frame, and if relativistic, then the electric and magnetic fields are computed using potential, phi, and velocity of source for potential, beta. This function must be defined in the derived classes.

Implemented in EffectivePotentialES, LabFrameExplicitES, and RelativisticExplicitES.

◆ InitData()

virtual void ElectrostaticSolver::InitData ( )
inlinevirtual

Reimplemented in EffectivePotentialES, LabFrameExplicitES, and RelativisticExplicitES.

◆ operator=() [1/2]

ElectrostaticSolver & ElectrostaticSolver::operator= ( const ElectrostaticSolver & )
delete

◆ operator=() [2/2]

ElectrostaticSolver & ElectrostaticSolver::operator= ( ElectrostaticSolver && )
delete

◆ ReadParameters()

void ElectrostaticSolver::ReadParameters ( )

◆ setPhiBC()

void ElectrostaticSolver::setPhiBC ( ablastr::fields::MultiLevelScalarField const & phi,
amrex::Real t ) const

Set Dirichlet boundary conditions for the electrostatic solver. The given potential's values are fixed on the boundaries of the given dimension according to the desired values from the simulation input file, boundary.potential_lo and boundary.potential_hi.

Parameters
[in,out]phiThe electrostatic potential
[in]tcurrent time

Member Data Documentation

◆ is_igf_2d_slices

bool ElectrostaticSolver::is_igf_2d_slices = false

Parameters for FFT Poisson solver aka IGF

◆ m_poisson_boundary_handler

std::unique_ptr<PoissonBoundaryHandler> ElectrostaticSolver::m_poisson_boundary_handler

Boundary handler object to set potential for EB and on the domain boundary

◆ num_levels

int ElectrostaticSolver::num_levels

Maximum levels for the electrostatic solver grid

◆ self_fields_absolute_tolerance

amrex::Real ElectrostaticSolver::self_fields_absolute_tolerance = 0.0

◆ self_fields_max_iters

int ElectrostaticSolver::self_fields_max_iters = 200

Limit on number of MLMG iterations

◆ self_fields_required_precision

amrex::Real ElectrostaticSolver::self_fields_required_precision = 1e-11

Parameters for MLMG Poisson solve

◆ self_fields_verbosity

int ElectrostaticSolver::self_fields_verbosity = 2

Verbosity for the MLMG solver. 0 : no verbosity 1 : timing and convergence at the end of MLMG 2 : convergence progress at every MLMG iteration

The documentation for this class was generated from the following files:
Generated by doxygen 1.13.2